精心整理弹簧设计规范一、弹簧的功能弹簧是一种弹性元件，由于材料的弹性和弹簧的结构特点，它具有多次重复地随外栽荷的大小而做相应的弹性变形，卸载后立即恢复原状的特性。

　　其主要功能有：⑴、减振和缓冲，如车辆的悬挂弹簧，各种缓冲器和弹性联轴器中的弹簧等。

　　⑶、储存及输出能量，如钟表弹簧，枪栓弹簧，仪表和自动控制机构上的原动弹簧等。

　　三、弹簧使用的材料及其用途弹簧钢的的主要性能要求是高强度和高屈服极限和疲劳极限，所以弹簧钢材用较高的含碳量。

　　碳素钢用于直径较小的弹簧，工艺多为冷拔成型，如：65#，75#，85#。

　　直径稍大，需用热成型工艺生产的弹簧多采用60Si2Mn，如汽车板簧，铁路车辆的缓冲簧。

　　对于高应力的重要弹簧可采用50CrV,常用于高级轿车板簧，发动机气门弹簧等。

　　a、碳钢及合金钢：制造弹簧时，常加矽、锰、铬、钒及钼等金属元素于钢中，以增加弹簧之弹性及疲劳限度，且使其耐冲击。

　　因此要求弹簧材料具有较高的抗拉强度极限、弹性极限和疲劳强度极限，不易松弛。

　　弹簧的伸长量与原长度的关系-概述说明以及解释1.引言1.1 概述:弹簧作为一种常见的机械零件，其在各个领域都有着广泛的应用。

　　弹簧的伸长量与原长度的关系对于我们了解弹簧的性能和工作原理具有重要意义。

　　本文旨在探讨弹簧的伸长量与原长度的关系，通过分析弹簧的基本原理和计算方法，深入探讨弹簧的伸长量与原长度之间的数学关系，为我们更好地理解和应用弹簧提供理论支持。

　　通过本文的研究，我们可以更好地设计和选择弹簧，并在实际应用中更好地发挥其作用。

　　json{1.2 文章结构: {本文将从弹簧的基本原理、弹簧的伸长量计算方法和弹簧伸长量与原长度的关系这三个方面展开讨论。

　　接着，将详细介绍弹簧的伸长量计算方法，包括受力分析、弹簧常数的影响因素等内容。

　　最后，将重点讨论弹簧伸长量与原长度的关系，探讨不同表现形式下弹簧伸长量与原长度的变化规律。

　　通过这三个方面的介绍，可以全面了解弹簧的伸长量与原长度的关系，为读者提供一种清晰的认识和理解途径。

　　}}1.3 目的本文的目的在于探究弹簧的伸长量与其原长度之间的关系。

　　通过对弹簧的基本原理、伸长量计算方法以及伸长量与原长度的关系进行详细分析和讨论，旨在帮助读者深入理解弹簧的性质和特点，为工程设计和实际应用提供参考依据。

　　通过本文的研究,读者将了解到弹簧在不同条件下的伸长情况，有助于在实际工程中选择合适的弹簧材料和设计合理的弹簧结构，提高弹簧的使用效率和性能。

　　2.正文2.1 弹簧的基本原理弹簧是一种能够存储和释放弹性势能的机械元件，常用于各种机械装置中，如悬挂系统、减震系统、压缩弹簧等。

　　弹簧一般由金属丝或金属带材制成，根据形状和用途的不同，可以分为压缩弹簧、拉伸弹簧和扭转弹簧等多种类型。

　　弹簧的基本原理是根据胡克定律，即弹簧的伸长或压缩量与施加在其上的力成正比。

　　机械密封弹簧是一种常见的机械密封元件，广泛应用于各种工业设备中，用于防止介质泄漏。

　　机械密封弹簧是一种用于机械密封装置中的重要零部件，其主要作用是通过弹性变形来保持密封件的紧密接触，从而防止介质泄漏。

　　在实际工作中，机械密封弹簧通常处于受压状态，因此其长度的设计和计算至关重要。

　　机械密封弹簧长度的计算公式通常基于弹簧的材料、截面形状、工作条件等因素进行推导。

　　在实际工程中，常用的机械密封弹簧长度计算公式如下：L = (Fmax Fmin) / k。

　　其中，L为机械密封弹簧的长度；Fmax为最大工作力；Fmin为最小工作力；k 为弹簧刚度系数。

　　在实际工程中，可以根据具体的工作条件和要求，通过该公式来计算机械密封弹簧的长度，从而满足设计和制造的需求。

　　机械密封弹簧长度计算公式的应用涉及到多个方面，包括弹簧材料的选择、弹簧结构的设计、弹簧工作状态的分析等。

　　不同的材料具有不同的弹性模量和屈服强度，因此在计算机械密封弹簧的长度时，需要考虑材料的特性。

　　通常情况下，弹簧材料的弹性模量越大，长度计算公式中的弹簧刚度系数k就越大，从而导致弹簧长度变短。

　　例如，弹簧的截面形状、横截面积等参数都会影响其弹性变形特性，进而影响其长度计算。

　　因此，在设计机械密封弹簧时，需要充分考虑其结构特点，以便准确计算其长度。

　　机械密封弹簧在工作过程中通常处于受压状态，因此需要对其工作状态进行分析，以确定最大工作力和最小工作力。

　　拉伸弹簧计算公式弹簧是一种能够储存和释放能量的弹性体，广泛应用于机械、汽车、电子等领域。

　　在工程设计中，计算拉伸弹簧的性能参数是非常重要的，而拉伸弹簧的计算公式则是关键的工具之一。

　　拉伸弹簧的计算公式可以帮助工程师确定弹簧的弹性系数、最大拉伸长度、最大负荷等重要参数，从而确保弹簧在实际应用中能够正常工作并符合设计要求。

　　在了解拉伸弹簧的计算公式之前，我们首先需要了解一些与弹簧相关的基本参数。

　　拉伸弹簧的基本参数包括弹簧系数（k）、最大拉伸长度（L）、最大负荷（Fmax）等。

　　弹簧系数是衡量弹簧刚度的重要参数，它表示单位长度内弹簧所受的拉力与位移的比值，通常用N/m或lb/in表示。

　　最大拉伸长度是指弹簧在最大负荷下的拉伸长度，而最大负荷则是弹簧所能承受的最大拉力。

　　根据胡克定律，拉伸弹簧的弹性力可以表示为F=kx，其中F表示拉力，k表示弹簧系数，x表示弹簧的位移。

　　在实际应用中，通常使用下面的公式来计算弹簧系数：k = (Fmax F0) / (L L0)。

　　其中，k表示弹簧系数，Fmax表示最大负荷，F0表示无负荷时的拉力，L表示最大拉伸长度，L0表示无负荷时的长度。

　　通过这个公式，我们可以根据弹簧的最大负荷和拉伸长度来计算出弹簧系数，从而为后续的设计和计算提供基础数据。

　　最大拉伸长度是指弹簧在最大负荷下的拉伸长度，它可以通过下面的公式计算得到：L = (Fmax F0) / k。

　　通过这个公式，我们可以根据弹簧系数、最大负荷和无负荷时的拉力来计算出弹簧在最大负荷下的拉伸长度。

　　汽车变截面钢板弹簧的设计计算东风汽车工程研究院 陈耀明 2006年5月前 言少片变截面钢板弹簧在我国已有多年的制造和使用经验，特别是大、中型客车，采用者相当广泛。

　　然而，涉及变截面簧的设计计算方法，虽然二十几年前悬架专委会曾做过一些介绍，但资料零散、重复、不完整，尤其是比较常用的加强型变截面簧，资料反而欠缺。

　　撰写本文的目的，就是为悬架设计者提供变截面簧的比较完整的设计计算资料，主要是刚度计算公式和应力分布计算方法。

　　变截面簧轮廓线包括梯形和抛物线形两大类，每类又含有根部、端部加厚，或只有根部加厚，或都不加厚等几种变型。

　　此外，本文还介绍了各种轮廓线的选型原则以及若干设计经验等，可供设计人员参考。

　　本文的式（1）～（3）引自日本资料“自动车用重型钢板弹簧”，其它公式（6）～（15）是笔者近期重新推导出来的。

　　一、 纵截面为梯形的变截面弹簧这种弹簧的轧锥部分（3l ～4l 段）为梯形，而根部和端部都将厚度增大，称为加强型变截面簧，见图1。

　　弹簧设计规范(全)弹簧是一种弹性元件，具有多次重复地随外部载荷而做相应的弹性变形，卸载后立即恢复原状的特性。

　　它在很多机械中都发挥着重要的作用，主要包括减振和缓冲、测力、储存及输出能量、控制运动等功能。

　　根据所承受的载荷和形状的不同，弹簧可以分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧等四种类型，以及螺旋弹簧、碟形弹簧、环形弹簧、盘形弹簧和板弹簧等不同形状。

　　弹簧钢的主要性能要求是高强度、高屈服极限和疲劳极限，因此通常使用含碳量较高的钢材。

　　在各种弹簧中，圆柱螺旋弹簧是最常用的，因此本章将主要介绍这类弹簧的结构形式、设计理论和计算方法。

　　通过合理的设计和选择合适的材料，可以使弹簧发挥最佳的性能，满足各种特殊要求。

　　直径稍大，需要用热成型工艺生产的弹簧多采用60Si2Mn，例如汽车板簧、铁路车辆的缓冲簧。

　　对于高应力的重要弹簧，可以采用50CrV，常用于高级轿车板簧、发动机气门弹簧等。

　　制造弹簧时，常向钢中加入矽、锰、铬、钒及钼等金属元素，以增加弹簧的弹性和疲劳限度，并使其耐冲击。

　　大型弹簧多用热作加工，即将弹簧材料高温轧成棒，再高温加工成形后，淬火于780度～850度左右的油或水中，再施以400度～500度的温度回火。

　　小型弹簧则先经过退火，再用冷作加工，捲成后再经硬化回火，例如钢丝、琴钢丝或钢带。

　　琴钢丝是属于高炭钢材（0.65～0.95%）制造，杂质少，直径常小于1/4时经过轫化处理后在常温抽成线。

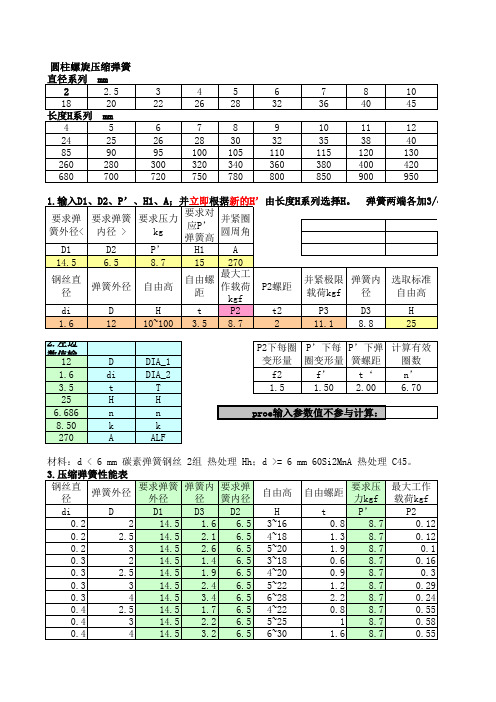
　　如图所示，圆柱弹簧的主要尺寸有：弹簧丝直径d、弹簧圈外径D、弹簧圈内径D1，弹簧圈中径D2，节距t、螺旋升角a、自由长度H0等。

　　K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）＝（８０００×２４）／（８×２０３×３．５）＝０．５７１ｋｇｆ／ｍｍ

　　压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；

　　弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；

　　弹簧常数公式（单位：kgf/mm）：K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）

　　G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300；磷青铜线 ；黄铜线

　　当拉伸弹簧受轴向拉力F时，弹簧丝槽剖面上的受力情况和压缩弹簧相同，只是扭矩T和切向力Q均为相反的方向。所以上述两种弹簧的计算方法可以一并讲述。

　　从受力分析可见，弹簧受到的应力主要为扭矩和横向力引起的剪应力，对于圆形弹簧丝

　　1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。

　　2、仅部分预览的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。

　　3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

　　G抗拉强度σBkg/mm2查表螺旋升角 (5°~9°)K脉动疲劳极限τ0

　　本站资源均为网友上传分享，本站仅负责收集和整理，有任何问题请在对应网页下方投诉通道反馈